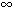 and n is zero,
+1 is returned.
and n is zero,
+1 is returned.
|
|
cc [flag . . .] file . . . -lm [library . . .]#include <math.h>
double exp(double x);
float expf(float x);
long double expl(long double x);
double exp2(double x);
float exp2f(float x);
long double exp2l(long double x);
double ldexp(double x, int exp);
float ldexpf(float x, int exp);
long double ldexpl(long double x, int exp);
double frexp(double x, int *exp);
float frexpf(float x, int *exp);
long double frexpl(long double x, int *exp);
double expm1(double x);
float expm1f(float x);
long double expm1l(long double x);
double cbrt(double x);
float cbrtf(float x);
long double cbrtl(long double x);
double modf(double value, double *iptr);
float modff(float value, float *iptr);
long double modfl(long double value, long double *iptr);
double pow(double x, double y);
float powf(float x, float y);
long double powl(long double x, long double y);
double pown(double x, int n);
float pownf(float x, int n);
long double pownl(long double x, int y);
double scalbn(double x, int n);
float scalbnf(float x, int n);
long double scalbnl(long double x, int n);
double scalbln(double x, long int n);
float scalblnf(float x, long int n);
long double scalblnl(long double x, long int n);
double sqrt(double x);
float sqrtf(float x);
long double sqrtl(long double x);
exp2, exp2f and exp2l return 2^x.
ldexp, ldexpf and ldexpl return x x 2^exp.
frexp, frexpf and frexpl return x with a magnitude in the interval [1/2,1] or is equal to zero and value equal to x x 2^exp. If value is zero, bith parts of the result are also zero. If value is not a floating-point number, the results are unspecified.
expm1, expm1f and expm1l return e^x - 1.0.
cbrt, cbrtf and cbrtl return the cube root of x.
modf, modff and modfl return the signed fractional part of value.
pow, powf and powl return x^y. If x is zero, y must be non-negative. If x is negative, y must be an integer.
pown, pownf and pownl return
x^n. If x is zero,
n must be non-negative. If x is an NaN
or is ±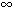 and n is zero,
+1 is returned.
and n is zero,
+1 is returned.
scalbn, scalbnf and scalbnl return x x FLT_RADIX^n.
scalbln, scalblnf and scalblnl return x x FLT_RADIX^n.
sqrt, sqrtf and sqrtl return the non-negative square root of x. The value of x must not be negative.
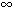 and set errno to ERANGE.
exp, expf and expl return
+0 if x is -
and set errno to ERANGE.
exp, expf and expl return
+0 if x is -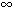 and set errno to ERANGE.
and set errno to ERANGE.
exp2, exp2f and exp2l return a value
that compares equal to HUGE_VAL,
HUGE_VALF or HUGE_VALL
when the correct value
would overflow, or zero when the correct value would underflow,
and set errno to ERANGE.
exp2, exp2f and exp2l return
+HUGE_VAL,
+HUGE_VALF or +HUGE_VALL
if x is +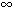 and set errno to ERANGE.
exp2, exp2f and exp2l return
+0 if x is -
and set errno to ERANGE.
exp2, exp2f and exp2l return
+0 if x is -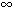 and set errno to ERANGE.
and set errno to ERANGE.
expm1, expmlf and expmll
return a value that compares equal to
HUGE_VAL,
HUGE_VALF or HUGE_VALL
when the correct value would overflow
and set errno to ERANGE.
expml, expmlf and expmll return
+HUGE_VAL,
+HUGE_VALF or +HUGE_VALL
if x is +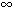 and set errno to ERANGE.
expml, expmlf and expmll return
-1 if x is -
and set errno to ERANGE.
expml, expmlf and expmll return
-1 if x is -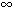 and set errno to ERANGE.
expml, expmlf and expmll return
NaN and set errno to EDOM if
x has the value NaN.
and set errno to ERANGE.
expml, expmlf and expmll return
NaN and set errno to EDOM if
x has the value NaN.
On systems that support IEEE NaN, if any of the inputs to each of these functions is a quiet NaN, that value is returned. If any input is a signaling NaN, a quiet NaN is returned and the invalid operation exception is raised. In either case, errno is set to EDOM. The only exceptions to this rule are for pow and powf, which always return 1 when their second argument is zero, regardless of the value of their first argument.
If x is negative and y is finite and nonintegral, pow, powf and powl return IEEE NaN on systems that support it and raise the invalid operation exception. Otherwise, they return zero and set errno to EDOM.
When x is zero and y is negative, finite and an odd integer, pow, powf and powl return a value that compares equal to ±HUGE_VAL, ±HUGE_VALF or ±HUGE_VALL according to the sign of x, (+HUGE_VAL, +HUGE_VALF or +HUGE_VALL if -0 is not supported). When x is zero and y is negative, finite and not an odd integer, pow, powf and powl return a value that compares equal to +HUGE_VAL, +HUGE_VALF or +HUGE_VALL. In each of these cases, errno is set to EDOM. On systems that support IEEE exceptions, the divide by zero exception is raised.
On systems that support IEEE infinity, when
x is ±1 and y is
±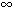 ,
pow, powf and powl return
IEEE NaN, raise the invalid operation exception and set
errno to EDOM.
,
pow, powf and powl return
IEEE NaN, raise the invalid operation exception and set
errno to EDOM.
When the correct value for pow, powf or powl would overflow or underflow, these functions return a value that compares equal to ±HUGE_VAL, ±HUGE_VALF or ±HUGE_VALL for overflow or zero for underflow, and set errno to ERANGE.
When x is +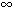 and n is
greater than zero pown, pownf and pownl
return a value that compares equal to +HUGE_VAL,
+HUGE_VALF or +HUGE_VALL.
When x is +
and n is
greater than zero pown, pownf and pownl
return a value that compares equal to +HUGE_VAL,
+HUGE_VALF or +HUGE_VALL.
When x is +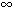 and n is
less than zero pown, pownf and pownl
return +0. In each of these cases, errno
is set to ERANGE.
and n is
less than zero pown, pownf and pownl
return +0. In each of these cases, errno
is set to ERANGE.
When x is -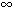 and n is
an odd positive pown, pownf and pownl
return a value that compares equal to -HUGE_VAL,
-HUGE_VALF or -HUGE_VALL.
When x is -
and n is
an odd positive pown, pownf and pownl
return a value that compares equal to -HUGE_VAL,
-HUGE_VALF or -HUGE_VALL.
When x is -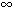 and n is
an even positive pown, pownf and pownl
return a value that compares equal to +HUGE_VAL,
+HUGE_VALF or +HUGE_VALL.
In each of these cases, errno
is set to ERANGE.
and n is
an even positive pown, pownf and pownl
return a value that compares equal to +HUGE_VAL,
+HUGE_VALF or +HUGE_VALL.
In each of these cases, errno
is set to ERANGE.
When x is -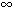 and n is
an odd negative pown, pownf and pownl
return -0. When x is -
and n is
an odd negative pown, pownf and pownl
return -0. When x is -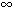 and n is
an even negative pown, pownf and pownl
return +0. In each of these cases, errno
is set to ERANGE.
and n is
an even negative pown, pownf and pownl
return +0. In each of these cases, errno
is set to ERANGE.
When x is ±0 and n is an odd negative, pown, pownf and pownl return a value that compares equal to ±HUGE_VAL, ±HUGE_VALF or ±HUGE_VALL according to the sign of x, (+HUGE_VAL, +HUGE_VALF or +HUGE_VALL if -0 is not supported). When x is ±0 and n is an even negative, pown, pownf and pownl return a value that compares equal to +HUGE_VAL, +HUGE_VALf OR +HUGE_VALl. In each of these cases, errno is set to EDOM. On systems that support IEEE exceptions, the divide by zero exception is raised.
When x is negative, sqrt, sqrtf and sqrtl return IEEE NaN on systems that support it and raise the invalid operation exception. Otherwise, they return 0. errno is set to EDOM.
If the program was compiled with the -Xt compilation mode, a value that will compare equal to ±HUGE is returned instead of ±HUGE_VAL. pow, powf and powl return zero and set errno to EDOM when x is 0 and y is non-positive, or when x is negative and y is non-integral. In addition, a message indicating DOMAIN error is printed on the standard error output. pown, pownf and pownl return zero and set errno to EDOM when x is ±0 and n is negative. sqrt, sqrtf and sqrtl return zero and set errno to EDOM when x is negative. In addition, a message indicating DOMAIN error is printed on the standard error output. These error handling procedures can be changed with the function matherr.
AT&T SVID Issue 2;
X/Open Portability Guide Issue 4, Version 2 (Spec-1170);
IEEE POSIX Std 1003.1-1990 System Application Program Interface
(API) [C Language] (ISO/IEC 9945-1);
and NIST FIPS 151-2.
expm1 is conformant with:
X/Open Portability Guide Issue 4, Version 2 (Spec-1170).
pow and sqrt are conformant with:
AT&T SVID Issue 2;
X/Open Portability Guide Issue 4, Version 2 (Spec-1170);
ANSI X3.159-1989 Programming Language -- C;
IEEE POSIX Std 1003.1-1990 System Application Program Interface
(API) [C Language] (ISO/IEC 9945-1);
and NIST FIPS 151-2.